Activating Prior Knowledge in
I've been tutoring a 4th Grade Student who is being taught math using the "Math Expressions" program by Houghton Mifflin Harcourt. Chapter 2 explores ways to draw multiplication using area of rectangles, using Expanded Notation, using Algebraic Notation, using the Distributive Property, the Shortcut method, and the Place Value Section Method. YIKES, each page is a different method!!
To help her, I've decided to concentrate on ONLY seven problems featuring - 1 digit X 2 digit problems.
That way she can use her schema to make connections between the different methods, instead of calculating new problems for each method.
What Is Schema?
Call it schema, relevant background knowledge, prior knowledge, or just plain experience, when students make connections to the mathematics they are learning, their understanding increases. Good mathematicians constantly try to make sense out of what they are learning by seeing how it fits with what they already know. Ellin Oliver Keene and Susan Zimmerman in Mosaic of Thought (1997).
To begin with we activated her basic facts background knowledge by completing these expressions. This can serve as math bank of facts while working on the calculation in the lessons to follow. These same facts will be needed throughout each method. As I work with her, it isn't about knowing your facts... but about understanding the deeper meaning about the impact of the place value of the digit when you multiply multi-digit numbers.
I had pre-cut the following 4 pages into number expression strips, area model drawings, and corresponding real life word problems.
I asked her to explain her thinking about her choice. She did so.
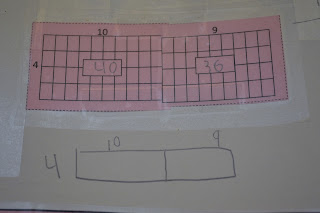
She has already covered expanded form of numbers and quickly defined 14 as 10 + 4. I then explained that we were going to show her thinking using an area model of square unit by using the number 14 in that expanded form.
While "thinking out-loud," I chose these 2 area models. I explained that each square represents an apple and quickly sketched in some apples in some of the square units on the model.
To record our thinking, I glued the strip containing the math expression and the area model onto her paper.
The above page was placed in a clear plastic worksheet protector, and I completed my calculations, using a dry erase marker, while "thinking out-loud" and explained the WHY behind my calculations. I recorded my calculations next to the model on her large sheet of paper.
 |
| Using the Place Value Model with a Quick Rectangle |
 Moving on to the distributive property model..... The area model that we had already completed helped her understand how 6 X 14 could be redistributed into 6 X 10 and 6 X 4, while not changing the amount in any way.
Moving on to the distributive property model..... The area model that we had already completed helped her understand how 6 X 14 could be redistributed into 6 X 10 and 6 X 4, while not changing the amount in any way.
The new learning came from explaining the use of " ( )" to record our thinking. She found it funny that the + sign was stuck there in the middle of all those ( )'s. With a bit of help, she wrote down all the math equations for the SAME 6 problems.
and work on the next method- Algebraic Notation Method and substitute a dot for the previously used X symbol.
The beauty of continuing to glue our thinking onto the same piece of paper really was like magic. She used her schema to see the slight change in the equation and plunged on to calculate the SAME 6 problems again using this method. "The word Algebra kind of scared me, but it's really not that big of a difference is it?" she said.
The beauty of continuing to glue our thinking onto the same piece of paper really was like magic. She used her schema to see the slight change in the equation and plunged on to calculate the SAME 6 problems again using this method. "The word Algebra kind of scared me, but it's really not that big of a difference is it?" she said.
 |
| From My Teacher Pay Teacher Store |
Smiles,
Deborah















No comments :
Post a Comment